Construcción de un camino de datos
Una forma razonable de comenzar un diseño de un camino de datos es examinar los componentes principales necesarios para ejecutar cada tipo de instrucción MIPS. Comencemos examinando qué elementos del camino de datos necesita cada instrucción y construyamos las secciones del camino de datos para cada tipo de instrucción a partir de estos elementos. Cuando inicialmente mostremos los elementos del camino de datos, también mostraremos sus señales de control. Después de eso, no incluiremos las señales de control en el camino de datos real hasta la Sección 5.3, donde añadimos la unidad de control.
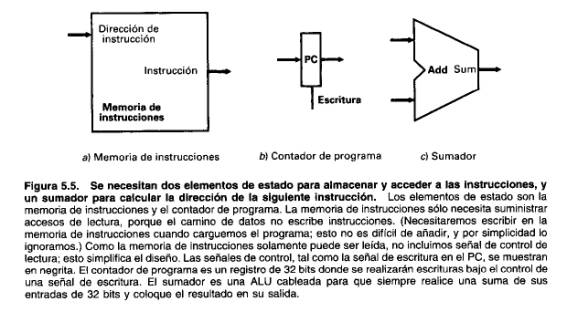
El primer elemento que necesitamos es un dispositivo para almacenar las instrucciones de un programa. Una unidad de memoria, que es un elemento de estado, se utiliza para que contenga y suministre instrucciones dada una dirección, como muestra la Figura 5.5.La dirección de la instrucción también debe estar en un elemento de estado, que llamaremos contador de programa (PC), que también se muestra en la Figura 5.5. Finalmente, necesitaremos un sumador para incrementar el PC a la dirección de la siguiente instrucción. Este sumador, que es combinacional, puede construirse a partir de la ALU diseñada en el último capítulo, conectando sencillamente las líneas de control para que el control especifique siempre una operación de suma. Dibujaremos esta ALU con el rótulo Add, como en la Figura 5.5, para indicar que se ha convertido permanentemente en un sumador y no puede realizar las demás funciones de la ALU.

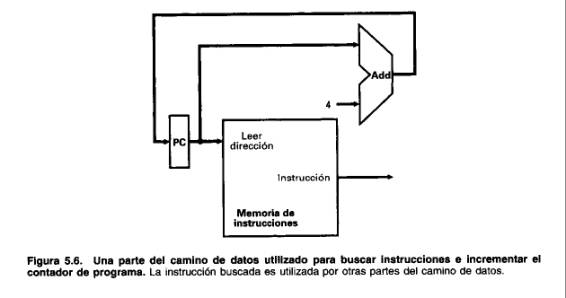
Para ejecutar cualquier instrucción debemos comenzar buscando la instrucción en memoria. Para preparar la ejecución de la siguiente instrucción, también debemos incrementar el contador de programa en 4 bytes para que apunte a la siguiente instrucción. El camino de datos para este paso, mostrado en la Figura 5.6, utiliza los tres elementos de la Figura 5.5.
Consideremos ahora las instrucciones de formato R. Todas leen dos registros, realizan una operación en la ALU sobre los contenidos de los registros y escriben el resultado. Llamamos a estas instrucciones o instrucciones tipo R o instrucciones aritmético-lógicas (ya que realizan operaciones aritméticas o lógicas). Esta clase de instrucción incluye add, sub, and, or y s l t; recordar que un ejemplo típico de estas instrucciones es add $1, $2, $3, que lee $2 y $3 y escribe en $1. Los 32 registros del procesador se almacenan en una estructura denominada archivo de registros. Un archivo de registros es una colección de registros en los cuales cualquier registro puede ser leído o escrito especificando el número de registro en el archivo. El archivo de registros contiene el estado de los registros de la máquina. Además, necesitaremos una ALU para operar sobre los valores leídos en los registros.
Debido a que las instrucciones de formato R tienen tres operandos de registro, para cada instrucción necesitaremos leer dos palabras de datos del archivo de registros y escribir una palabra de datos en el archivo de registros: Para leer cada palabra de dato de los registros, necesitamos una entrada al archivo de registros que especifique el número del registro que se va a leer y una salida del archivo de regitros que lleve el valor que se ha leído en el registro. Para escribir una palabra de dato, necesitamos dos entradas: una para especificar el número del registro donde se va a escribir y otra para suministrar el dato que se va a escribir en el registro. Por tanto, necesitamos un total de cuatro entradas (tres para números de registro y una para dato) y dos salidas (ambas para datos), como muestra la Figura 5.7 El archivo de registros siempre saca el contenido de cualquier número de registro que se encuentra en las entradas Leer de los registros. Sin embargo, las escrituras están controladas por la señal de control de escritura, que debe estar asertada para que se produzca una escritura cuando cae la entrada de reloj. Las entradas de los números de registro son de 5 bits para especificar uno de los 32 registros (32 = 2e5), mientras que la entrada de dato y las dos salidas de datos son cada una de 32 bits. La ALU necesita dos entradas de 32 bits y produce un resultado de 32 bits: La ALU, mostrada en la Figura 5.7, está controlada por una señal de 3 bits .

El camino de datos para estas instrucciones tipo R, que utilizan el archivo de registros y la ALU de la Figura 5.7 se muestra en la Figura 5.8. Como los números de registros provienen de campos de instrucción, mostramos la instrucción, que proviene de la Figura 5.6, cuando se conecta a las entradas de los registros del archivo de registros.

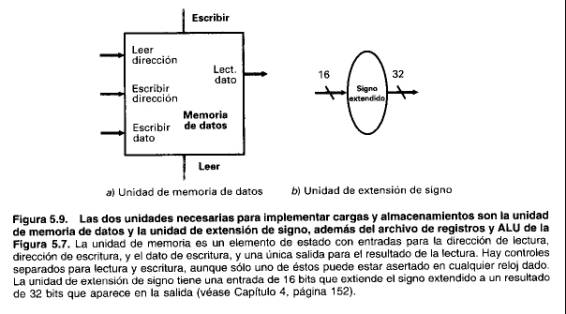
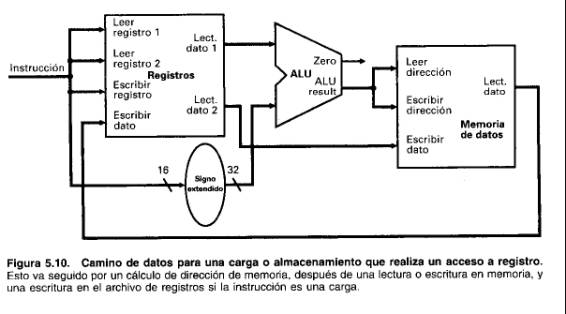
A continuación consideramos las instrucciones de carga y almacenamiento de MIPS, que tienen la forma general: lw$l, desplazamiento ($2) o sw $1, desplazamiento ($2). Estas instrucciones calculan una dirección de memoria sumando el registro base ($2) al campo de desplazamiento (offset) de 16 bits con signo, contenido en la instrucción. Si la instrucción es un almacenamiento, el valor que se va a almacenar también debe ser leído en el archivo de registros ($1). Si la instrucción es una carga, el valor leído en memoria debe ser escrito en el archivo de registros en el registro especificado ($1). Así, para las instrucciones de formato R necesitaremos tanto el archivo de registros como la ALU, y se muestran en la Figura 5.7. Además necesitaremos una unidad para el signo extendido del campo de desplazamiento de 16 bits de la instrucción a un valor de 32 bits con signo, y una unidad de memoria de datos para lecturas y escrituras. En la memoria de datos realizan escrituras las instrucciones de almacenamiento; por consiguiente, tiene señales de control para lectura y para escritura, así como una entrada para el dato que se va a escribir en memoria. La Figura 5.9 muestra estos dos elementos.
La Figura 5.10 muestra cómo combinar estos elementos para construir el camino de datos para una instrucción de cargar palabra o almacenar palabra, suponiendo que la instrucción ya ha sido buscada. Las entradas de los números de registro para el archivo de registros provienen de los campos de la instrucción, como ocurre con el valor de desplazamiento, que después de la extensión del signo se convierte en la segunda entrada de la ALU.
La instrucción beq tiene tres operandos, dos registros que se comparan para la igualdad, y un desplazamiento de 16 bits utilizado para calcular la dirección destino del salto con respecto a la dirección de la instrucción de salto. Su forma es beq $1, $2, despLazamiento: Para implementar esta instrucción, debemos calcular la dirección destino del salto sumando el campo de desplazamiento con signo extendido de la instrucción al PC: Como se observó en la elaboración del Capítulo 3, hay dos detalles en la arquitectura del repertorio de instrucciones a los que debemos prestar atención.
· La arquitectura del repertorio de instrucciones especifica que la base para el cálculo de las direcciones de los saltos es la dirección de la instrucción siguiente al salto. Como calculamos PC + 4 (la dirección de la instrucción siguiente) en el camino de datos del ciclo de búsqueda de la instrucción, es fácil utilizar este valor como base para calcular la dirección destino del salto.
· La arquitectura también establece que el campo de desplazamiento se desplace 2 bits a la izquierda para que sea un desplazamiento de palabra; este desplazamiento es útil porque incrementa el rango efectivo del campo de desplazamiento en un factor de 4.
Para tratar con la última complicación, necesitaremos desplazar el campo de desplazamiento en dos. Esto se hace en el primer dibujo del camino de datos que aparece en la Figura 5.11, que muestra el camino de datos del salto. (Más tarde también necesitaremos ajustar los desplazamientos de las bifurcaciones.)
Además para calcular la dirección de destino del salto, también debemos determinar si la siguiente instrucción es la instrucción que sigue en secuencia o la instrucción de la dirección del destino del salto: Cuando la condición es verdadera (por ejemplo, los operandos son iguales), la dirección de destino del salto se convierte en el nuevo valor del PC, y decimos que se realiza el salto. Si los operandos no son iguales, el PC incrementado debe sustituir al PC actual (igual que para cualquier otra instrucción normal); en este caso decimos que no se realiza el salto.
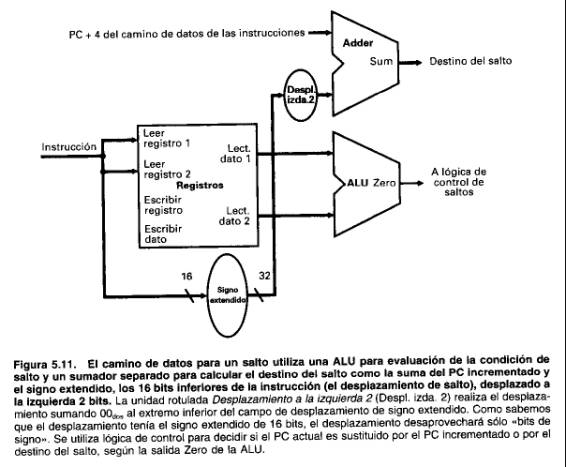
Así, el salto debe hacer dos operaciones: calcular la dirección de destino del salto y comparar el contenido de los registros. Para calcular la dirección de destino del salto necesitaremos una unidad de extensión de signo, como la de la Figura 5.9, y un sumador. También debemos modificar la parte de búsqueda de la instrucción del camino de datos. Para realizar la comparación, necesitamos utilizar el archivo de registros mostrado en la Figura 5.7 para suministrar los operandos de los dos registros (aunque no necesitaremos escribir en el archivo de registros). Además, la comparación puede hacerse utilizando la ALU que diseñamos en el Capítulo 4. Como esa ALU proporciona una señal de salida que indica si el resultado era O, podemos enviar los operandos de los dos registros a la ALU con el control inicializado para realizar una resta. Si la señal Zero (Cero) que sale de la ALU está asertada, sabemos que los dos valores son iguales. Aunque la salida Zero siempre indica si el resultado es O, la utilizaremos sólo para implementar el test de igualdad en los saltos. Más tarde, mostraremos exactamente cómo conectar las señales de control de la ALU para utilizarlas en el camino de datos. El camino de datos para un salto combina estos elementos, como se muestra en la Figura 5.11.
La instrucción de bifurcación opera sustituyendo una parte del PC por los 26 bits inferiores de la instrucción desplazada a la izquierda 2 bits. Este desplazamiento (shift) se realiza sencillamente concatenando 00 al desplazamiento (offset) de la bifurcación.
Ahora que hemos examinado los caminos de datos necesarios para los tipos individuales de instrucción, podemos combinarlos en un solo camino de datos y añadir el control para completar la implementación. Los caminos de datos mostrados en las Figuras 5.6, 5.8, 5.10 y 5.11 serán bloques de construcción para dos implementaciones diferentes. En la sección siguiente crearemos una implementación que utiliza un solo ciclo de reloj para cada instrucción: En la Sección 5.4 examinaremos una implementación que utiliza múltiples ciclos de reloj para cada instrucción.
Un
sencillo esquema de implementación
En esta sección contemplamos lo que podría considerarse la implementación más sencilla posible de nuestro subconjunto MIPS. Construimos este sencillo camino de datos y control ensamblando los segmentos de los caminos de datos de la última sección y añadiendo líneas de control cuando sea necesario. Esta sencilla implementación cubre las instrucciones cargar palabra (lw), almacenar palabra (sw), saltar si igual (beq), y las instrucciones aritméticológicas add, sub, and, or y slt. Más tarde mejoraremos el diseño para incluir una instrucción de bifurcación (j).
Suponer que fuésemos a construir un camino de datos utilizando las piezas que examinamos en las Figuras 5.6, 5.8, 5.10 y 5.11. El camino de datos más sencillo podría ejecutar todas las instrucciones en un ciclo de reloj. Esto significa que ningún recurso del camino de datos puede ser utilizado más de una vez por instrucción y que cualquier elemento que se necesite más de una vez debe estar duplicado. Por tanto, necesitamos una memoria para las instrucciones separada de la de los datos. Aunque algunas unidades funcionales necesitan estar duplicadas cuando se combinen los caminos de datos individuales de la sección anterior, muchos elementos pueden ser compartidos por diferentes flujos de instrucciones. Para compartir un elemento del camino de datos entre dos tipos de instrucciones diferentes, puede que se necesiten múltiples conexiones a la entrada de un elemento y una señal de control para seleccionar las entradas. Normalmente esto se hace con un dispositivo denominado multiplexor, aunque una denominación mejor seria selector de datos: El multiplexor, que fue introducido en el último capítulo (Figura 4.7 ), realiza una selección entre varias entradas en base a los valores de sus líneas de control.
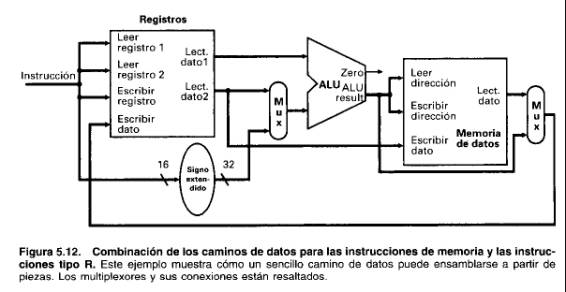
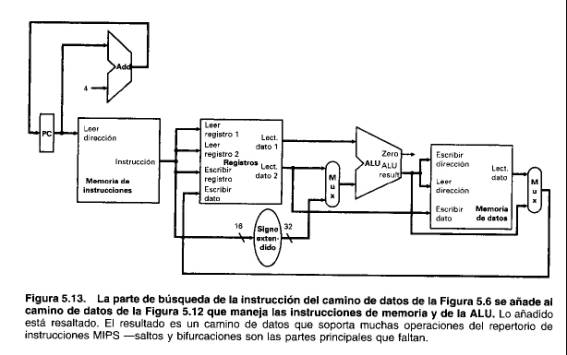
La parte de búsqueda de la instrucción del camino de datos, que se muestra en la Figura 5.6 de la página 244, puede añadirse fácilmente al camino de datos de la Figura 5.12: La Figura 5.13 muestra el resultado: El camino de datos combinado incluye una memoria para instrucciones y una memoria separada para datos. Este camino de datos combinado requiere un sumador y una ALU, ya que el sumador se utiliza para incrementar el PC, mientras que la otra ALU se utiliza para ejecutar la instrucción en el mismo ciclo de reloj.
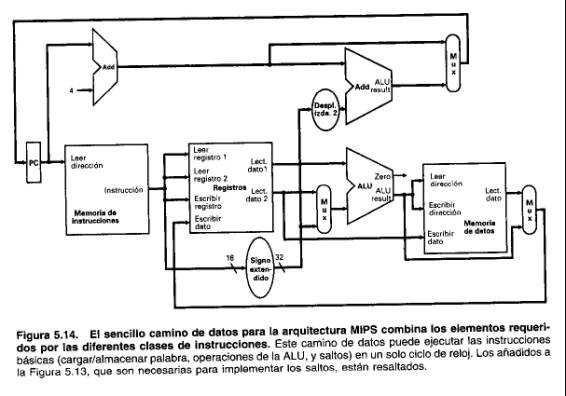
Ahora podemos combinar todas las piezas para hacer un camino de datos sencillo para la arquitectura MIPS añadiendo el camino de datos para saltos de la Figura 5.11. La Figura 5.14 muestra el camino de datos que obtenemos componiendo las piezas separadas. La instrucción de salto utiliza la ALU principal para la comparación de los operandos de los registros; asi, debemos mantener el sumador de la Figura 5.1.1 para calcular la dirección de destino del salto. Se necesita un multiplexor adicional para seleccionar o la dirección de la siguiente instrucción secuencial (PC + 4) o la dirección de destino del salto que se escribirá en el PC: Como en el PC se escribirá uno de estos dos valores en cada reloj, no necesitamos ninguna señal de control explícita para la escritura.
Ahora que hemos completado este sencillo camino de datos, podemos añadir la unidad de control: La unidad de control debe ser capaz de tomar las entradas y generar una señalde escritura para cada elemento de estado, el control del selector para cada multiplexor, y el control de la ALU. El control de la ALU es diferente en algunos aspectos, y se utilizará para diseñarlo primero, antes que diseñemos el resto de la unidad de control.
El control de la ALU
Recordar del Capítulo 4 que la ALU tiene tres entradas de control. Sólo se utilizan cinco de las ocho posibles combinaciones de entradas. La Figura 4.19 mostraba las cinco combinaciones siguientes:

Podemos generar la entrada de control de 3 bits de la ALU utilizando una pequeña unidad de control que tiene como entradas el campo de función de la instrucción y un campo de control de 2 bits, que llamamos ALU0p: ALU0p indica si la operación que se va a realizar debe ser sumar (00) para cargas y almacenamientos, restar (01) para beq, o la operación codificada en el campo de función (10). La salida de la unidad de control de la ALU es una señal de 3 bits que controla directamente la ALU generando una de las cinco combinaciones de 3 bits mostradas en la página anterior. En la Figura 5.15 vemos cómo inicializar las entradas de control de la ALU en base al control ALUOp de 2 bits yel código de función de 6 bits. Para completar, también se conoce la relación entre los bits de ALUOp y el código de operación de la instrucción: Más tarde en este capítulo veremos cómo se generan los bits de ALUOp a partir de la unidad de control principal.
Hay varias formas diferentes de implementar la correspondencia del campo ALU Op de 2 bits y el campo de código de función de 6 bits con los tres bits de control de operación de la ALU Debido a que sólo un pequeño número de los 64 valores posibles del campo de función son de interés y el campo de función se utiliza solamente cuando los bits de ALUOp son 10, podemos utilizar una pequeña parte de lógica que reconozca el subconjunto de posibles valores y realice la inicialización correcta de los bits de control de la ALU. Un paso útil en el diseño de esta lógica es crear una tabla de verdad para las combinaciones interesantes del campo de código de función y los bits de ALUOp como hemos hecho en la Figura 5.16; esta tabla de verdad muestra cómo el control de 3 bits de la ALU se inicializa dependiendo de estos campos de dos entradas. Como la tabla de verdad completa es muy grande (27 = 128 entradas) y el control de la ALU es 000 para la mayor parte de estas combinaciones de entrada, mostramos sólo las entradas de la tabla de verdad para las cuales el control de la ALU es distinto de 000. A lo largo de este capítulo utilizaremos esta práctica de mostrar sólo las entradas de la tabla de verdad que tienen valores de salida distintos de cero. (Esta práctica tiene una desventaja que explicaremos en breve.)
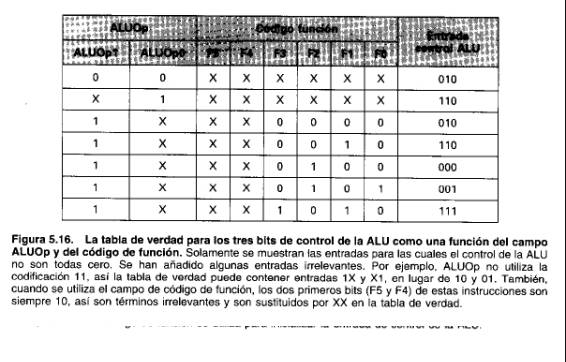
Como en muchas circunstancias no nos importan los valores de algunas entradas y para mantener las tablas compactas, también incluimos estos términos «irrelevantes». Un término irrelevante (representado por X) en esta tabla de verdad indica que la salida es cierta, independientemente del valor de la entrada correspondiente: Por ejemplo, cuando los bits de ALUOp son 00, como en la primera línea de la tabla de la Figura 5.16, siempre inicializamos el control de la ALU a 010, independientemente del código de función. Entonces, en este caso las entradas del código de función serán irrelevantes en esta línea de la tabla de verdad: Más tarde veremos ejemplos de otro tipo de término irrelevante.
Una vez que se ha construido la tabla de verdad, puede optimizarse y después ser convertida a puertas. Este proceso es completamente mecánico: La optimización se aprovecha de los irrelevantes de la tabla.
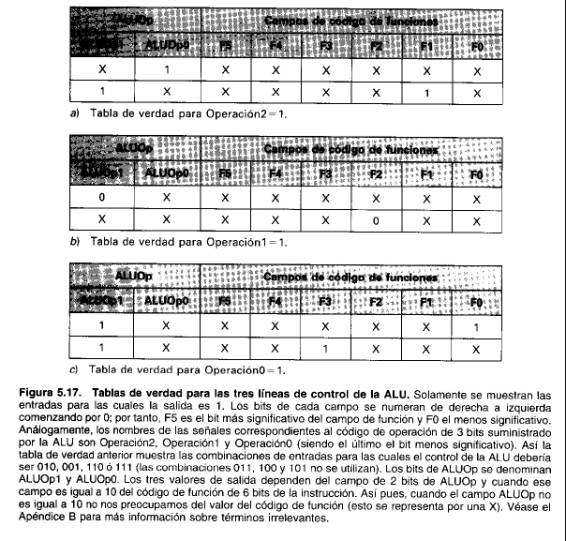
Un bloque lógico que implemente la función de control de la ALU tendrá tres salidas distintas (llamadas Operación2, Operación 1 y OperaciónO), cada una corresponde a uno de los tres bits de control de la ALU. La función lógica para cada salida se construye combinando todas las entradas de la tabla de verdad que inicializan (ponen a 1) esa salida particular. Por ejemplo, el bit de orden inferior del control de la ALU (OperaciónO) se pone a 1 por las dos últimas entradas de la tabla de verdad de la Figura 5. 16. Por tanto, la tabla de verdad para OperaciónO tendrá estas dos entradas: Además, la observación de las tablas de verdad para cada salida individualmente nos permite minimizar la lógica requerida para explotar lo común entre los términos asociados a una salida. La Figura 5.17 muestra las tablas de verdad para cada uno de los tres bits de control de la ALU Nos hemos aprovechado de la estructura común de cada tabla de verdad al incorporar irrelevantes adicionales: Por ejemplo, las cinco líneas de la tabla de verdad de la Figura 5.16 que inicializa Operaciónl se reducen a dos entradas en la Figura 5.17. Un programa de minimización lógica utilizará los términos irrelevantes para reducir el número de puertas y el número de entradas a cada puerta en una implementación de puertas lógicas de estas tablas de verdad.
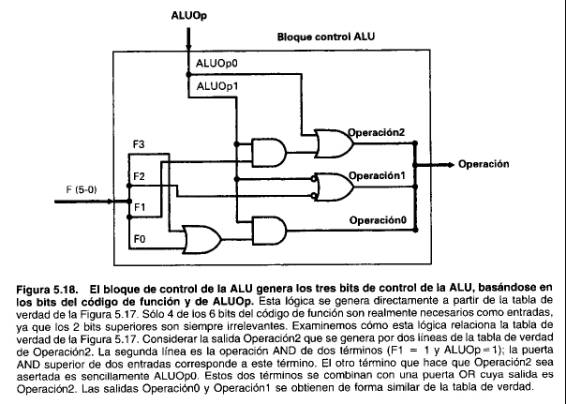
A partir de la tabla de verdad simplificada en la Figura 5. 17 podemos generar la lógica mostrada en la Figura 5.18 que denominamos bloque de control ALU. Este proceso es sencillo y puede hacerse con un programa de diseño asistido por computador (CAD). Un ejemplo de cómo las puertas lógicas pueden obtenerse a partir de las tablas de verdad se da en la leyenda de la Figura 5.18.
Esta lógica de control de la ALU es simple porque sólo hay tres salidas, y sólo necesitan ser reconocidas algunas de las posibles combinaciones de entrada. Si un gran número de posibles códigos de función de la ALU tuviesen que ser transformados en señales de control de la ALU, este sencillo método no sería eficiente. En lugar de ello se podría utilizar un decodificador, una memoria, o un array estructurado de puertas lógicas. Estas técnicas se describen con detalle en los Apéndices B y C.
Elaboración: En general, una ecuación lógica y la representación de Ia tabla de verdad de una función lógica son equivalentes. (Explicamos esto con más detalle en el Apéndice B.) Sin embargo, cuando una tabla de verdad sólo especifica Ias entradas que producen salidas no-cero, puede no describir completamente la función lógica. Una tabla de verdad completamente llena indica todas las entradas irrelevantes. Por ejemplo, codificar 11 para ALUOp siempre genera un término irrelevante en la salida. Por tanto, una tabla de verdad completa debería tener XXX en Ia parte de salida para todas las entradas con 11 en eI campo ALUOp. Estas entradas irrelevantes nos permiten sustituir al campo ALUOp 10 y 01 con lX y Xl, respectivamente. Incorporar los términos irrelevantes y minimizar la lógica es complejo y propenso a errores y, por tanto, es mejor dejarlo a un programa.
Diseño de la
unidad de control principal
.Ahora que hemos descrito cómo diseñar una ALU que utilice el código de función y una señal de 2 bits como entrada de control, podemos examinar el resto del control. Para comenzar este proceso, identifiquemos todas las líneas de control y los componentes de la instrucción requeridos para el camino de datos que construimos en la Figura 5.14 . Para comprender cómo se deben añadir los buses para encaminar las partes de la instrucción al camino de datos, es útil revisar los formatos de los tres tipos de instrucciones: las instrucciones tipo R, de salto y de carga/almacenamiento. Estos formatos se muestran en la Figura 5.19.

Hay algunas observaciones importantes sobre este formato de instrucción:
· El campo op, también llamado el código de operación, está siempre contenido en los bits 31-26. Nos referiremos a este campo como Op[50].
· Los dos registros que se van a leer están siempre especificados por los campos rs y rt, en las posiciones 25-21 y 20-16. Esto es cierto para las instrucciones tipo R, saltar sobre igual y almacenar.
· El registro base para las instrucciones de carga y almacenamiento está siempre en las posiciones de los bits 2521 (rs).
· El desplazamiento de 16 bits para saltar sobre igual, cargar y almacenar está siempre en las posiciones 15-0.
· El registro destino está en una de dos posiciones. Para una instrucción de carga está en las posiciones de los bits 20- 16 (rt), mientras que para una instrucción tipo R está en las posiciones de los bits 1511 (rd). Por tanto, necesitaremos añadir un multiplexor que seleccione el campo de la instrucción que indique el número del registro donde se va a escribir.
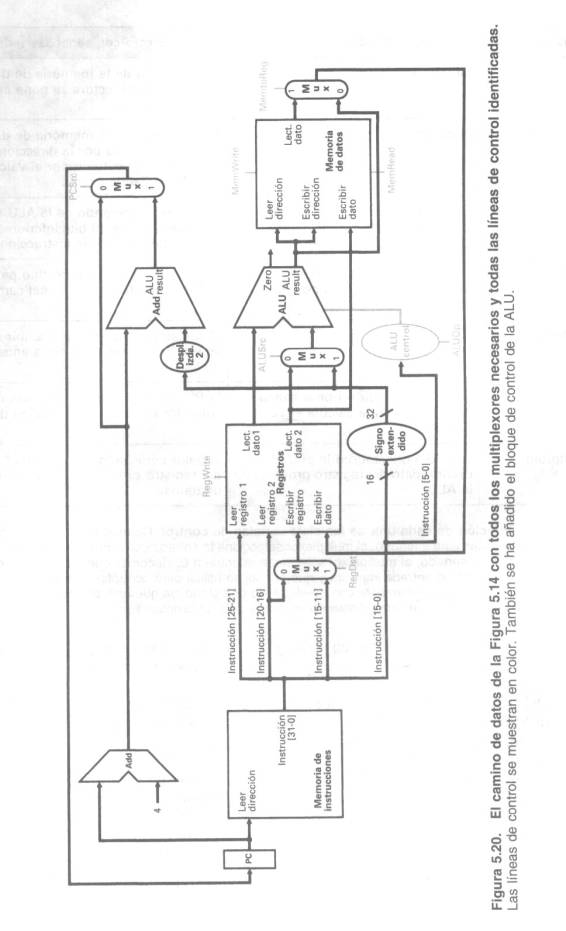
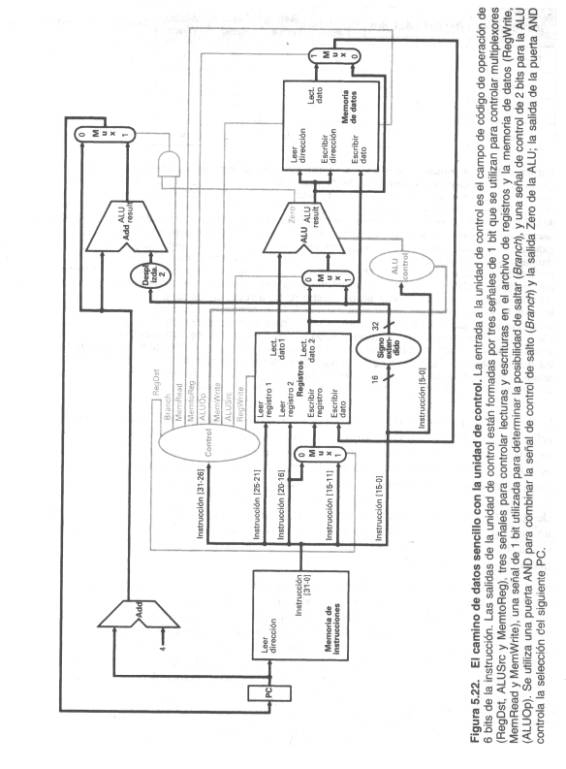
Utilizando esta información podemos añadir los rótulos de las instrucciones y el multiplexor extra (para la entrada Write del número de registro del archivo de registros) al camino de datos. La Figura 5.20 muestra estas adiciones más el bloque de control de la ALU, las señales de escritura para los elementos de estado, la señal de lectura para la memoria de datos y las señales de control para los multiplexores. Como todos los multiplexores tienen dos entradas, cada uno de ellos necesita una sola línea de control.
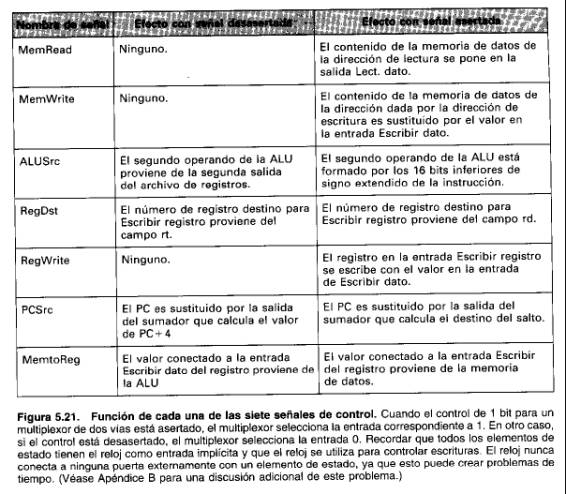
La Figura 5.20 muestra las siete líneas de control de un solo bit más la señal de control de 2 bits ALUOp. Ya hemos definido cómo funciona la señal de control ALUOp, y es útil definir informalmente lo que hacen las otras siete señales de control antes de inicializar estas señales de control durante la ejecución de las instrucciones. La Figura 5.21 describe la función de estas siete líneas de control.
Una vez que hemos examinado la función de cada una de las señales de control, intentaremos inicializarlas: La unidad de control puede inicializar todo excepto una de las señales de control, basándose únicamente en el campo de código de operación de la instrucción: La línea de control PCSrc es la excepción. Esa línea de control debería inicializarse si la instrucción es saltar sobre igual (una decisión que la unidad de control puede realizar) y la salida Zero de la ALU, que se utiliza para la comparación de la igualdad, es verdadera. Para generar la señal PCSrc, necesitaremos realizar la operación AND de una señal de la unidad de control, que llamamos Branch (Saltar), con la señal Zero de salida de la ALU.
Estas nueve señales de control pueden ahora inicializarse en base a las seis señales
de entrada a la unidad de control, que son los bits del código de operación:
El camino de datos con la unidad de control y las señales de control se
muestran en la Figura 5.22.
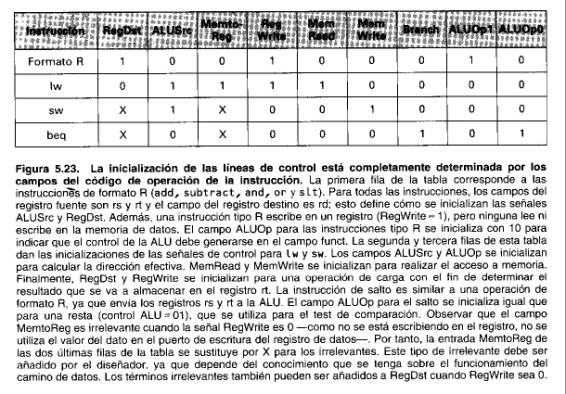
Antes de intentar escribir un conjunto de ecuaciones o una tabla de verdad para la unidad de control, será útil definir informalmente la función de control. Como la inicialización de las líneas de control depende solamente del código de operación, definimos el valor que debe tener cada señal de control 0, 1, o irrelevante (X), para cada uno de los campos de interés del código de operación: La Figura 5.23 define cómo deberían inicializarse las señales de control para los códigos de operación; esta información se obtiene directamente de las Figuras 5.15, 5.21 y 5.22.
Con la información de las Figuras 5.21 y 5.23 podemos diseñar la lógica de la unidad de control, pero antes de hacer eso, examinemos cómo utiliza cada instrucción el camino de datos. En las siguientes figuras mostramos el flujo de tres tipos de instrucciones diferentes a través del camino de datos. Las señales de control asertadas y los elementos activos del camino de datos aparecen resaltados en cada una de ellas. Observar que un multíplexor cuyo control es 0 tiene una accíón defínida, íncluso sí su línea de control no está resaltada: Las señales de control de múltíples bits aparecen resaltadas sí cualquier señal constituyente es asertada.
Comencemos con una ínstrucción tipo R, como add $x, $y, $z. En lugar de considerar el camino de datos completo como una parte de la lógica combinacional, es más fácil pensar que una instrucción se ejecuta en una seríe de pasos, centrando nuestra atención en la parte del camino de datos asociada a cada paso. Los cuatro pasos para ejecutar una ínstruccíón tipo R son:
1. Se busca la instruccíón en la memoría de instrucciones y se incrementa el PC: La Figura 5.24 muestra este primer paso: Las unídades activas y las líneas de control asertadas están resaltadas; las que son asertadas en pasos posteriores de una instrucción tipo R están en gris, y las de gris claro son las no activas para una instrucción tipo R en cualquier paso. El mismo formato se sigue en los t tres pasos siguientes.
2. Del archivo de registros se leen dos registros, $y y $z, como muestra la Figura 5.25 . La unidad de control principal calcula la inicialización de las líneas de control también durante este paso.
3. La ALU opera sobre los datos leídos del archivo de registros, utilizando el código de función (bits 50 de la instrucción) para generar la funcion de la ALU. La Figura 5.26 de la página 266 muestra la operación de este paso.
4. El resultado de la ALU se escribe en el archivo de registros utilizando los bits 15-11 de la instrucción para seleccionar el registro destino ($x): La Figura 5.27 muestra el paso final añadido a los tres anteriores.
Recordar que esta implementación es combinacional: Es decir, no se trata de una serie de cuatro pasos distintos. El camino de datos opera realmente en un solo ciclo de reloj, y las señales en el camino de datos pueden variar de forma impredecible durante el ciclo de reloj. Las señales se estabilizan aproximadamente en el orden de los pasos dados antes, porque el flujo de la información sigue este orden. Así, la Figura 5.27 muestra no sólo la acción del último paso, sino esencialmente la operación del camino de datos completo cuando el ciclo del reloj finaliza realmente.
Podemos ilustrar la ejecución de una instrucción de cargar palabra, tal como lw $x, desplazamiento($y), en un estilo similar a la Figura 5.27. La Figura 5.28 de la página 268 muestra las unidades funcionales activas y las lineas de control asertadas para una carga: Podemos considerar que una instrucción de carga opera en cinco pasos (similar a la instrucción tipo R ejecutada en cuatro):
1. Se busca una instrucción en la memoria de instrucciones y se incrementa el PC.
2. Se lee el valor de un registro ($y) en el archivo de registros.
3: La ALU calcula la suma del valor leido del archivo de registros y los 16 bits inferiores de signo extendido de la instrucción (desplazamiento).
4. La suma de la ALU se utiliza como dirección para la memoria de datos.
5. El dato de la unidad de memoria se escribe en el archivo de registros; el registro destino está dado por los bits 20 16 de la instrucción ($x).
Finalmente, podemos ilustrar de la misma manera la operación de la instrucción saltar sobre igual, tal como beq $x, $y, desp lazamiento: Opera de forma muy parecida a una instrucción de formato R, pero la salida de la ALU se utiliza para determinar si el PC se escribe con PC + 4 o con la dirección destino del salto. La Figura 5.29 muestra los cuatro pasos de la ejecución:
1. Se busca una instrucción en la memoria de instrucciones y se incrementa el PC.
2: En el archivo de registros se leen los dos registros, $x y $y
3. La ALU realiza una resta con los valores de los datos leídos del fichero de registros. El valor de PC + 4 se suma a los 16 bits inferiores de signo extendido de la instrucción (desp lazami ento); el resultado es la dirección destino del salto.
4. El resultado Zero de la ALU se utiliza para decidir qué resultado del sumador se almacena en el PC.
En la sección siguiente examinaremos máquinas que son realmente secuenciales, a saber, aquéllas en las que cada uno de estos pasos se realiza en un ciclo de reloj distinto.
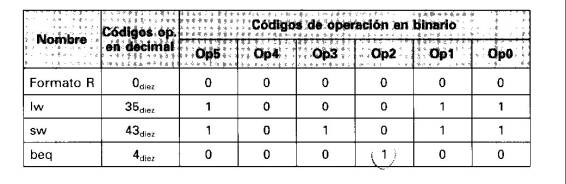
Ahora que hemos visto cómo las instrucciones operan en pasos, continuemos con la implementación del control. La función del control puede definirse precisamente utilizando los contenidos de la Figura 5.23. Las salidas son las líneas de control, la entrada es el campo de código de operación de 6 bits, Op [50]. Así podemos crear una tabla de verdad para cada una de las salidas: Antes de hacer eso, escribimos debajo la codificación para cada uno de los códigos de operación de interés de la Figura 5.23, como número decimal y como una serie de bits que son las entradas a la unidad de control:
Utilizando esta información, podemos ahora describir la lógica de la unidad de control en una gran tabla de verdad que combina todas las salidas como en la Figura 5.30 . Esta tabla especifica completamente la función de control, y podemos implementarla directamente con puertas de la misma forma que implementábamos la unidad de control de la ALU:
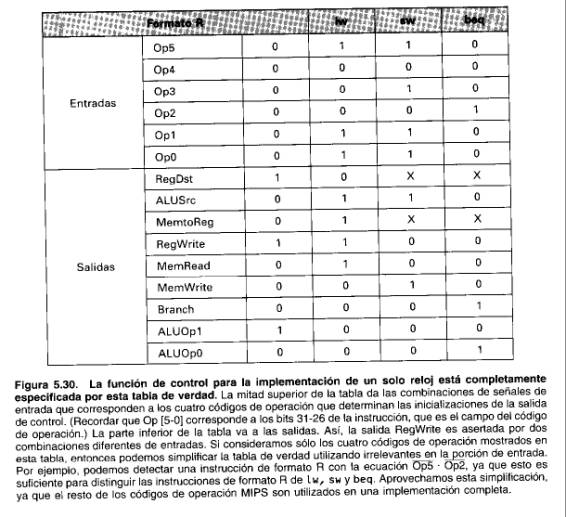
Implementar esta sencilla función con una colección no estructurada de puertas es razonable porque la función de control nunca es compleja ni grande. Sin embargo, si se utilizasen la mayor parte de los 64 códigos de operación posibles y hubiese muchas más líneas de control, el número de puertas sería mucho mayor y cada puerta podría tener muchas más entradas. Como cualquier función se puede calcular en dos niveles de lógica, otra forma de implementar una función lógica sería con un array lógico estructurado a dos niveles. La Figura 5.31 muestra tal implementación. Utiliza un array de puertas AND seguido por un array de puertas 0R: Esta estructura se denomina array lógico programable (PLA):
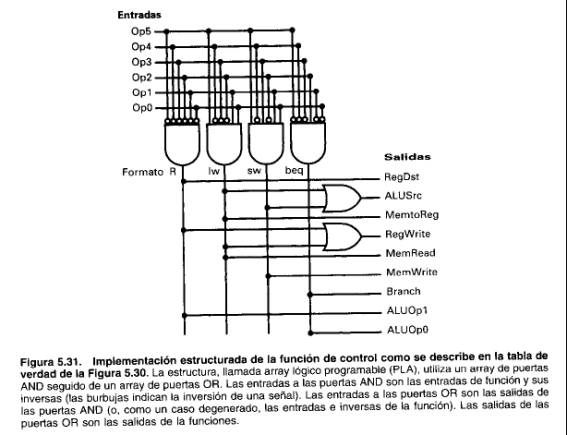
Un PLA es una de las formas más comunes de implementar una función de control: V olveremos al tópico de utilización de elementos lógicos estructurados para implementar el control más tarde en este capítulo; además esta cuestión también se trata en los Apéndices B y C.
Análogamente, si tuviésemos una máquina con modos de direccionamiento y operaciones más potentes, las instrucciones podrían variar desde tres o cuatro retardos de unidades funcionales a decenas o cientos de retardos de unidades funcionales. Además, como debemos asumir que el ciclo de reloj es igual al retardo del peor caso para todas las instrucciones, no podemos utilizar técnicas de implementación que reduzcan el retardo del caso común si no se mejora la duración del ciclo del peor caso. ¡ Por ejemplo, tal restricción haría que una caché fuese inútil en esta máquina! Una implementación de un solo ciclo entonces viola nuestro principio clave de diseño de hacer rápido el caso común . Además, con esta implementación de un solo ciclo, cada unidad funcional puede utilizarse s61o una vez por reloj; por tanto, algunas unidades funcionales deben estar duplicadas, elevando el coste de la implementación.
Podemos evitar estas dificultades utilizando técnicas de implementación que tengan un ciclo de reloj más corto -obtenido a partir de los retardos de las unidades funcionales básicas- y que requieran múltiples ciclos de reloj para cada instrucción: La siguiente sección explora este esquema alternativo de implementación: La segmentación solapa la ejecución de múltiples instrucciones para fomentar el aumento de rendimiento.