/*
* low_pass_filter.c -- Filtro paso bajo.
*
* Este fichero fuente puede encontrarse en:
* http://www.ace.ual.es/~vruiz/docencia/redes/practicas/low_pass_filter.c
*
* Compilar escribiendo (el paquete fftw debería estar instalado!):
* gcc low_pass_filter.c -o low_pass_filter -lfftw3 -lm
*
* Más información en: http/www.fftw.org
*
* gse. 2006
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <fftw3.h>
#include "spin.h"
main(int argc, char *argv[]) {
if(argc < 2) {
fprintf(stderr,
"%s cut-off_band signal.float > filtered_signal.float\n"
,argv[0]);
} else {
FILE *input_file = fopen(argv[2],"rb");
if(!input_file) {
fprintf(stderr,
"%s: unable to open input file \"%s\"\n",
argv[0],argv[2]);
exit(1);
}
int samples = compute_number_of_samples(input_file);
fprintf(stderr,"%s: number of samples = %d\n",argv[0],samples);
double *signal = (double *)fftw_malloc(samples*sizeof(double ));
fftw_complex *spectrum = (fftw_complex *)fftw_malloc(samples*sizeof(fftw_complex));
/* Creamos un plan para la transformada directa en inversa */
fftw_plan f = fftw_plan_dft_r2c_1d(samples, signal, spectrum, 0);
fftw_plan b = fftw_plan_dft_c2r_1d(samples, spectrum, signal, 0);
read_signal(signal, input_file, samples);
/* Calculamos la transformada de Fourier */
fftw_execute(f);
filter_signal(spectrum, atof(argv[1]), samples, argv);
/* Calculamos la transformada de Fourier inversa */
fftw_execute(b);
write_signal(signal, stdout, samples);
/* Destruímos los planes */
fftw_destroy_plan(f); fftw_destroy_plan(b);
/* Liberamos memoria */
free(spectrum);
free(signal);
}
return 0;
}
int compute_number_of_samples(FILE *input_file) {
fseek(input_file,0,SEEK_END);
int samples = ftell(input_file)/sizeof(float);
rewind(input_file);
return samples;
}
read_signal(double *signal, FILE *input_file, int samples) {
int i;
for(i=0; i<samples; i++) {
float x;
fread(&x,sizeof(float),1,input_file);
signal[i] = (double)x;
spin();
}
}
write_signal(double *signal, FILE *output_file, int samples) {
int i;
for(i=0; i<samples; i++) {
float sample = signal[i]/samples;
fwrite(&sample,sizeof(float),1,output_file);
spin();
}
}
filter_signal(fftw_complex *out, double factor, int samples, char **argv) {
int coefs_erased = 0; /* Coeficientes borrados */
int i;
int fmax = samples/2;
int bandas_eliminadas = fmax*(1.0-factor);
for(i=fmax-bandas_eliminadas; i<fmax; i++) {
out[i][0] = out[i][1] = 0.0;
coefs_erased++;
spin();
}
fprintf(stderr,"%s: number of erased Fourier coefficients = %d\n",
argv[0],coefs_erased);
fprintf(stderr,"%s: number of retained Fourier coeffcients = %d\n",
argv[0],samples/2-coefs_erased);
}
-
cut-off_band:
- es el índice, expresado como un número real entre 0 y 1, de la
banda de frecuencia más baja que es retenida (no eliminada). En general
este parámetro se calcula a partir de una frecuencia de corte (cut-off) fc
medida en Hz. Sea fs la frecuencia de muestreo (número de muestras por
segundo). Según el Teorema del Muestreo Uniforme, la máxima componente
de frecuencia de dicha señal no es superior a fs∕2. Entonces se cumple
que:

Supongamos, por ejemplo, que la señal digital transporta un bit de información por
segundo (esto significa que f0 = 1 Hz en la Figura 2.1). Si hemos tomado 32
muestras/bit, entonces tendremos fs = 32 muestras/segundo y que estamos
registrando hasta 16 Hz del espectro de dicha señal. Si queremos eliminar, por
ejemplo, la banda de frecuencias que va desde 8 Hz a 16 Hz, es decir, aplicar un
filtrado paso bajo:
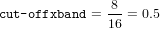
-
señal.float:
- es un fichero que almacena la señal a filtrar. Puesto que estamos
realizando los cálculos en una máquina digital, las señales deben estar digitalizadas
(muestreadas usando una frecuncia fs de muestreo constante y cuantificadas
utilizando un determinado número de bits).
-
filtered_signal.float:
- fichero que almacena la señal filtrada. La frecuencia de
muestreo y el número de bits por muestra son conservados. Por tanto,
los ficheros señal_original y señal_filtrada deben tener el mismo
tamaño.